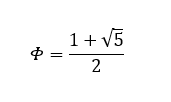Basic Concept of Fibonacci

Basic Concept of Fibonacci Trading Strategy

In writing this book I assumed that the reader has a fairly good knowledge of the Fibonacci numbers, and of the concepts of using Fibonacci in trading the markets. Nonetheless, I’m going to do a little review here in Chapter 1, just to refresh some of the ideas I’ll be building on later with the more advanced concepts. I’ll refrain from the detailed derivations of the number series and refer the reader to one of my introductory books on the subject, or to the many library and Internet references on the subject.

The most basic Fibonacci number is denoted as Phi (Φ), the ‘Golden Ratio’. It has a rounded value of 1.618. For those that like the mathematics behind this, you can get the exact value from this equation: 

The ratio 1.618:1 is pervasive all throughout the natural world. In studies on beauty performed across many cultures, the closer the different proportions of the face were to this ratio, the higher was the level of perceived beauty. If people are asked “which rectangles are the most pleasing to the eye”, the most preferred rectangular shape will have its longer side 1.618 times the length of its shorter side. The examples are endless. For those like myself who never tire of this, there are plenty of books available at the local library, not to mention resources on the Internet.

In my early days of exploring Fibonacci numbers, I was also fascinated with pi (π), the constant determined by dividing the circumference of a circle by its diameter. As we will see in a later chapter, pi can be used as an extreme external retracement for trading purposes. I was constantly thinking that pi and Phi must be related somehow, although I couldn’t begin to guess how two irrational numbers such as these could be joined in any kind of formula. Lo and behold, one day I found a reference to a mathematical proof that linked the two together into one complex formula. That was enough to solidify the concept, for me, that there was more going on in nature than meets the undiscerning eye.

Let’s look at the most commonly used Fibonacci numbers when it comes to trading. We already have Phi, the ‘golden ratio’, 1.618. We can derive many, many more numbers directly from this. For example, we can do the reciprocal, that is, flip 1.618 over, and we have .618. The .618 is denoted as phi (Φ) with a lowercase p in ‘phi’, as well as with the lowercase Greek letter Φ. This is, perhaps, the number that is the most well-known to the average person. Another example is to take the square roots of these two numbers, producing .786 and 1.272.

These four numbers, .618, .786, 1.272, and 1.618, are the ‘basic four’, the key numbers that most traders watch. Next, there is a lot of reference in the trading literature to .382. One of the nearly endless numbers of fascinating things about these Fibonacci numbers is how many different ways they can be derived from each other. So how can we get the .382? We can square .618 and we get .382. Or we can subtract .618 from 1 and get .382. There are other ways, but it’s sufficient to say you can spend many a rainy afternoon just finding new relationships and derivations if you are so inclined. 

The last of the common numbers you see being used for trading, or cited in the literature, are .500, 1.000 and 2.000. While none of these are ‘true’ Fibonacci numbers, they are used extensively in trading. The .500 would be the so-called ‘50% pullback’ or ‘50% retracement’. The 1.000 would correspond to the ‘double top’ or ‘double bottom’. These numbers will be included in the series I will build upon. In a later chapter, I will show that there are actual Fibonacci numbers (i.e., numbers derived directly from Phi) that are very close to these numbers. To the best of my knowledge, the introduction of these numbers in the context of trading will be a first.

This leaves the series that we will begin to work with at:

.382, .500, .618, .786, 1.000, 1.272, 1.618,2.000

While this may seem like a lot of numbers, most modern-day charting software allows all these and more to be pre-set, making their use quick and easy.