Fibonacci Projection
Internal Retracements, External retracements, Fibo Expansions, Fibonacci Retracements, Projections
Course: [ Advanced Fibonacci Trading Concept : Fibonacci Trading Strategy ]
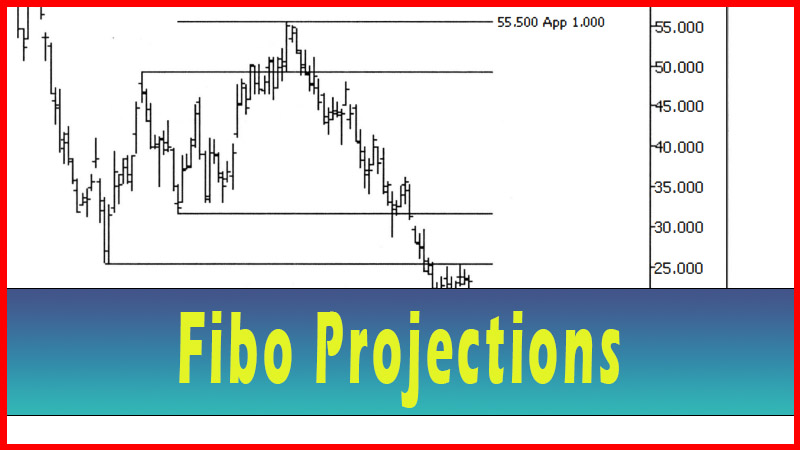
When I first began studying Fibonaccis, the concept of a projection took me quite a while to understand. In some ways this is a variation of a ‘measured move’. The idea is that if an issue makes a move and then rests, either by a pullback or some type of consolidation, and then starts to move again, the next move may be proportional to the first move in some way
Fibonacci Projections
When I first
began studying Fibonaccis, the concept of a projection took me quite a while to
understand. In some ways this is a variation of a ‘measured move’. The idea is
that if an issue makes a move and then rests, either by a pullback or some type
of consolidation, and then starts to move again, the next move may be
proportional to the first move in some way. In Elliot wave theory you have the
‘abc’ correction - where you get a move, a pullback and then a move equal to
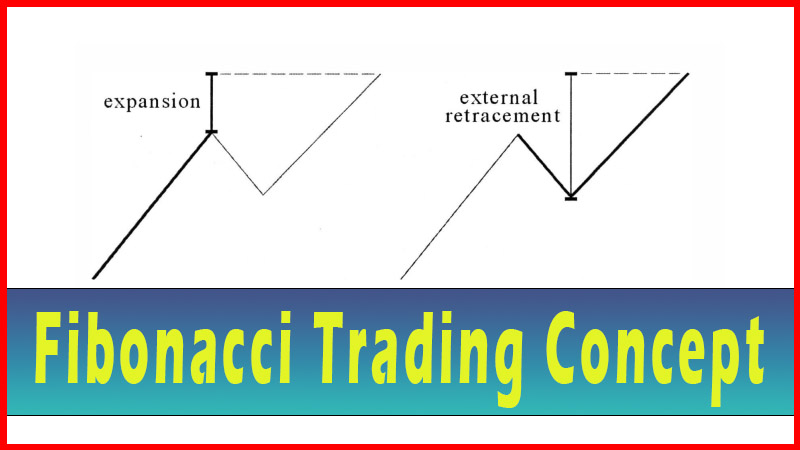
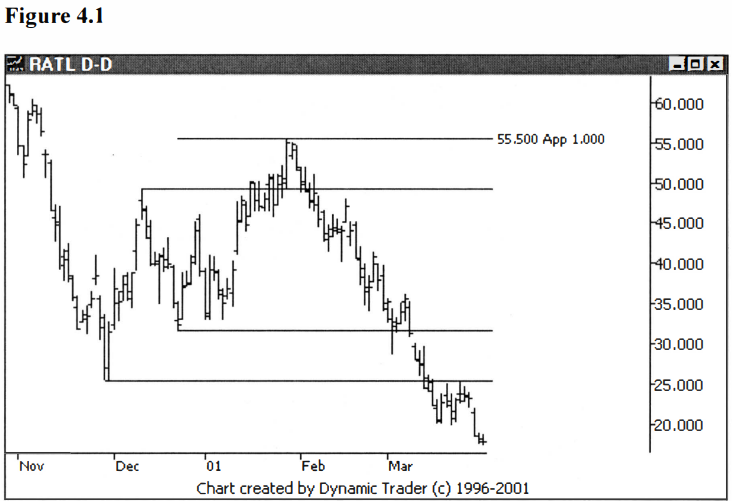
the first. See figure 4.1.
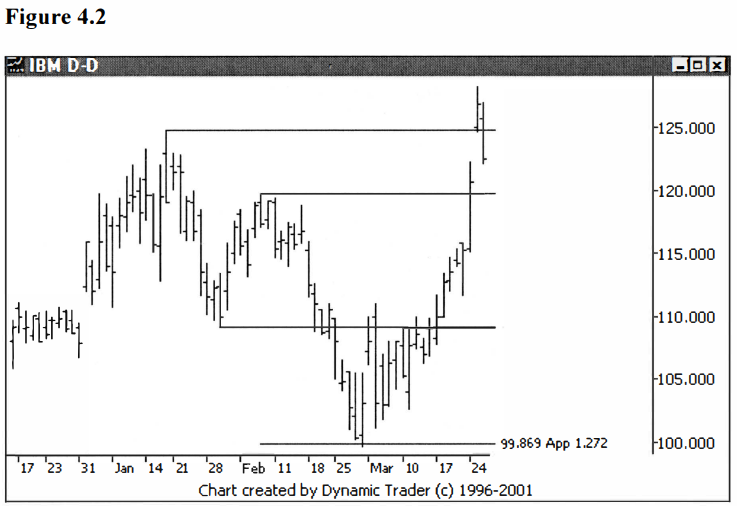
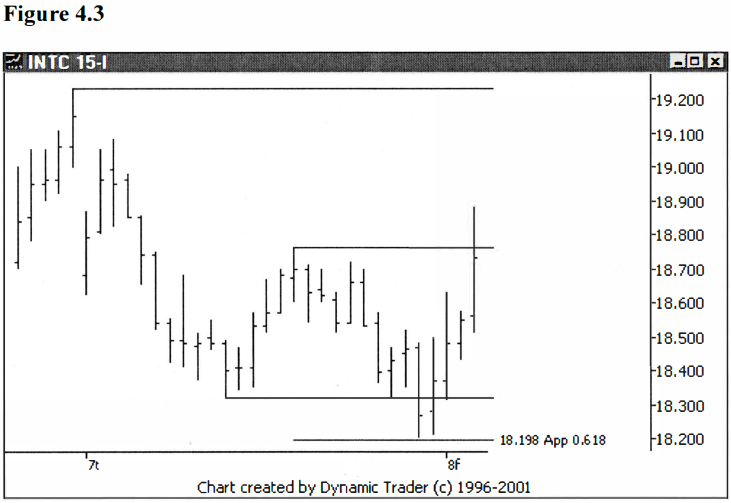
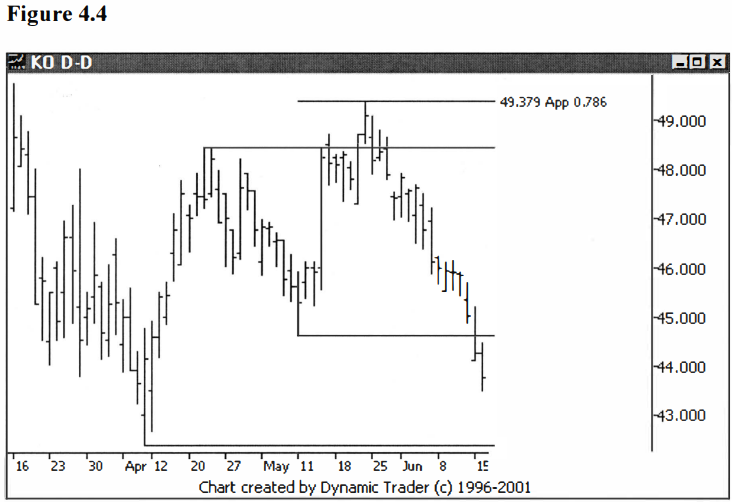
What I started to
notice was, in many of these moves, these zigzag or two- step corrections, the
two legs (the a and c legs in Elliot wave terms) weren’t equal. I did find,
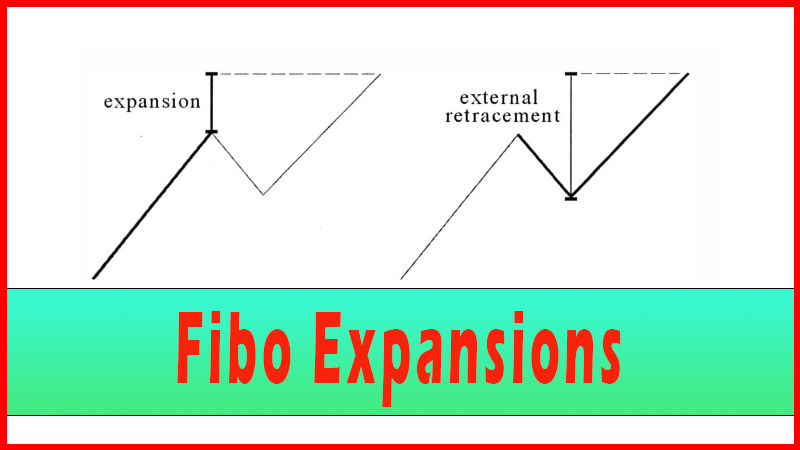
though, that they were frequently a Fibonacci ratio of each other. See figures
4.2-4.4.
This gave me more
areas to look at when I tried to determine a possible support or resistance
zone. Now, is this another example of traders discovering these numbers and
jumping the gun, while others try to drive them through the zones to pick off
stops? Possibly. For trading, my only concern is where the areas are that I
want to be looking at, not the why behind the moves.
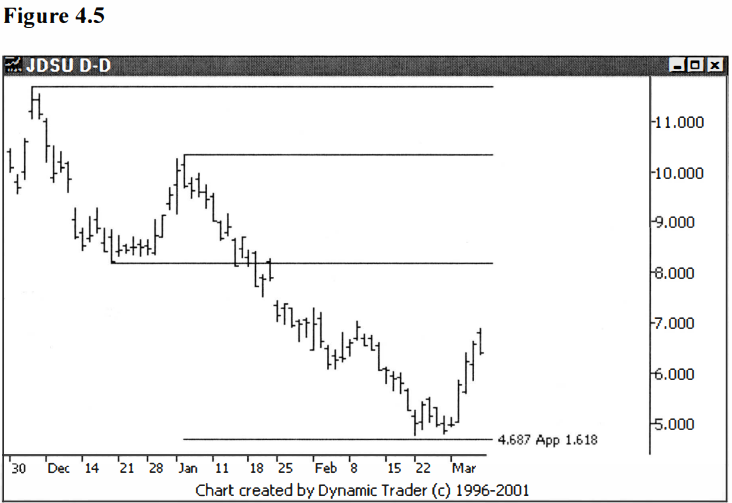
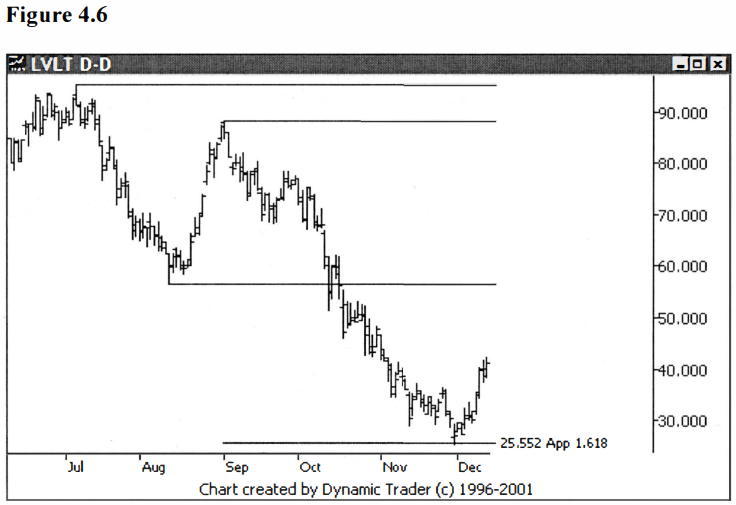
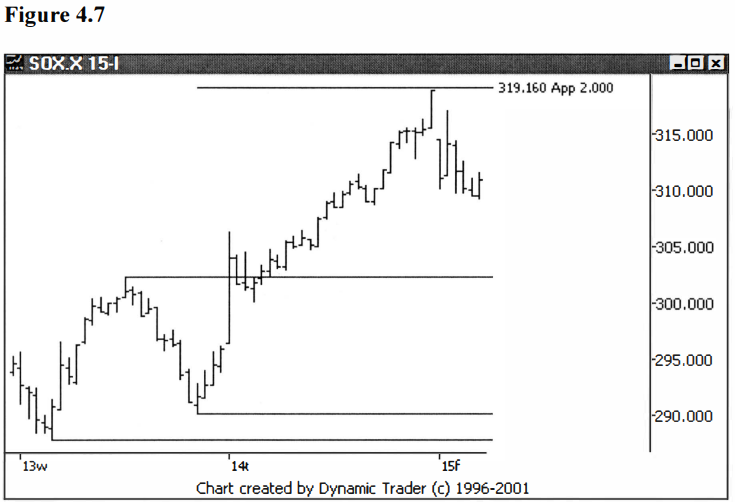
I’ve found the
idea of projections one of the most useful of all the Fibonacci concepts.
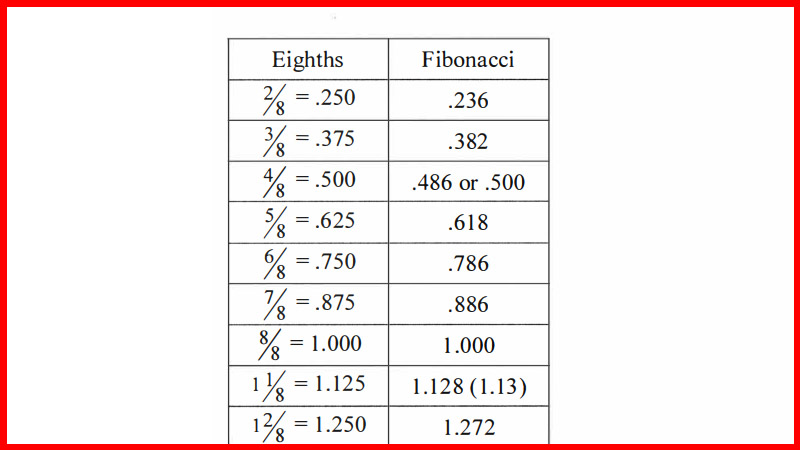
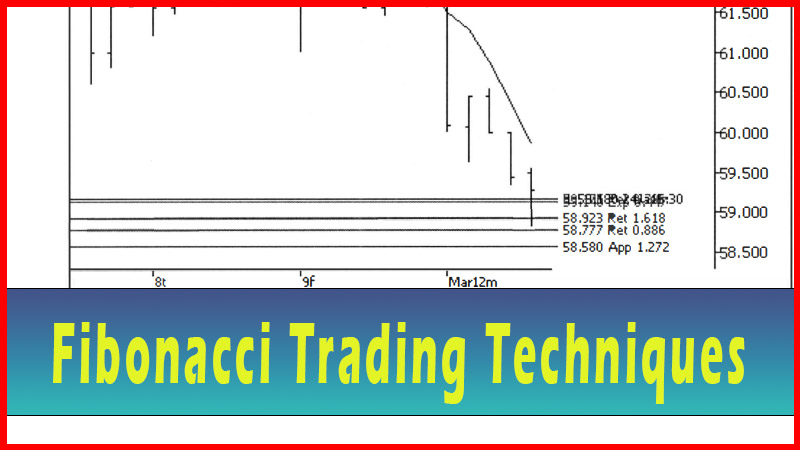
Generally, I find that in a correction to an existing trend, the move will be
close to an abc, with the a and c legs close to equal. The most common
projections to look for are .786, 1.000 and 1.272 projections. Once the c leg
is greater than 1.272 times the length of the a leg, I would start thinking
this is a new trend, not a correction anymore. In Elliot wave terms we would
then be in leg 3. I find these legs to project to 1.618 or 2.0 most commonly.
See figures 4.5-4.7.
Advanced Fibonacci Trading Concept : Fibonacci Trading Strategy : Tag: Fibonacci Trading, Forex : Internal Retracements, External retracements, Fibo Expansions, Fibonacci Retracements, Projections - Fibonacci Projection